Standard ML
| Paradigm(s) | multi-paradigm: functional, imperative |
|---|---|
| Typing discipline | strong, static, inferred |
| Major implementations | MLton, MLWorks, Moscow ML, Poly/ML, SML/NJ, SML.NET |
| Dialects | Alice, Dependent ML |
| Influenced by | ML |
Standard ML (SML) is a general-purpose, modular, functional programming language with compile-time type checking and type inference. It is popular among compiler writers and programming language researchers, as well as in the development of theorem provers.
SML is a modern descendant of the ML programming language used in the Logic for Computable Functions (LCF) theorem-proving project. It is distinctive among widely used languages in that it has a formal specification, given as typing rules and operational semantics in The Definition of Standard ML (1990, revised and simplified as The Definition of Standard ML (Revised) in 1997).[1]
Contents |
Language
Standard ML is a functional programming language with some impure features. Programs written in Standard ML consist of expressions to be evaluated, as opposed to statements or commands, although some expressions return a trivial "unit" value and are only evaluated for their side-effects.
Like all functional programming languages, a key feature of Standard ML is the function, which is used for abstraction. For instance, the factorial function can be expressed as:
fun factorial n =
if n = 0 then 1 else n * factorial (n-1)
A Standard ML compiler is required to infer the static type int -> int of this function without user-supplied type annotations. I.e., it has to deduce that n is only used with integer expressions, and must therefore itself be an integer, and that all value-producing expressions within the function return integers.
The same function can be expressed with clausal function definitions where the if-then-else conditional is replaced by a sequence of templates of the factorial function evaluated for specific values, separated by '|', which are tried one by one in the order written until a match is found:
fun factorial 0 = 1
| factorial n = n * factorial (n - 1)
This can be rewritten using a case statement like this:
val rec factorial =
fn n => case n of 0 => 1
| n => n * factorial (n - 1)
or as a lambda function:
val rec factorial = fn 0 => 1 | n => n * factorial(n -1)
Here, the keyword val introduces a binding of an identifier to a value, fn introduces the definition of an anonymous function, and case introduces a sequence of patterns and corresponding expressions.
Using a local function, this function can be rewritten in a more efficient tail recursive style.
fun factorial n = let
fun lp (0, acc) = acc
| lp (m, acc) = lp (m-1, m*acc)
in
lp (n, 1)
end
(The value of a let-expression is that of the expression between in and end.) The encapsulation of an invariant-preserving tail-recursive tight loop with one or more accumulator parameters inside an invariant-free outer function, as seen here, is a common idiom in Standard ML, and appears with great frequency in SML code.
Type synonyms
A type synonym is defined with the type keyword. Here is a type synonym for points in the plane, and functions computing the distances between two points, and the area of a triangle with the given corners as per Heron's formula.
type loc = real * real
fun dist ((x0, y0), (x1, y1)) = let
val dx = x1 - x0
val dy = y1 - y0
in
Math.sqrt (dx * dx + dy * dy)
end
fun heron (a, b, c) = let
val ab = dist (a, b)
val bc = dist (b, c)
val ac = dist (a, c)
val perim = ab + bc + ac
val s = perim / 2.0
in
Math.sqrt (s * (s - ab) * (s - bc) * (s - ac))
end
Algebraic datatypes and pattern matching
Standard ML provides strong support for algebraic datatypes. An ML datatype can be thought of as a disjoint union. They are easy to define and easy to program with, in large part because of Standard ML's pattern matching as well as most Standard ML implementations' pattern exhaustiveness checking and pattern redundancy checking.
A datatype is defined with the datatype keyword, as in
datatype shape = Circle of loc * real (* center and radius *) | Square of loc * real (* upper-left corner and side length; axis-aligned *) | Triangle of loc * loc * loc (* corners *)
(See above for the definition of loc.) Note: datatypes, not type synonyms, are necessary to define recursive constructors. (This is not at issue in the present example.)
Order matters in pattern matching; patterns that are textually first are tried first. Pattern matching can be syntactically embedded in function definitions as follows:
fun area (Circle (_, r)) = 3.14 * r * r | area (Square (_, s)) = s * s | area (Triangle (a, b, c)) = heron (a, b, c) (* see above *)
Note that subcomponents whose values are not needed in a particular computation are ellided with underscores, or so-called wildcard patterns.
The so-called "clausal form" style function definition, where patterns appear immediately after the function name, is merely syntactic sugar for
fun area shape =
case shape
of Circle (_, r) => 3.14 * r * r
| Square (_, s) => s * s
| Triangle (a, b, c) => heron (a, b, c)
Pattern exhaustiveness checking will make sure each case of the datatype has been accounted for, and will produce a warning if not. The following pattern is inexhaustive:
fun center (Circle (c, _)) = c | center (Square ((x, y), s)) = (x + s / 2.0, y + s / 2.0)
There is no pattern for the Triangle case in the center function. The compiler will issue a warning that the pattern is inexhaustive, and if, at runtime, a Triangle is passed to this function, the exception Match will be raised.
The set of clauses in the following function definition is exhaustive and not redundant:
fun hasCorners (Circle _) = false | hasCorners _ = true
If control gets past the first pattern (the Circle), we know the value must be either a Square or a Triangle. In either of those cases, we know the shape has corners, so we can return true without discriminating which case we are in.
The pattern in second clause the following (meaningless) function is redundant:
fun f (Circle ((x, y), r)) = x+y | f (Circle _) = 1.0 | f _ = 0.0
Any value that matches the pattern in the second clause will also match the pattern in the first clause, so the second clause is unreachable. Therefore this definition as a whole exhibits redundancy, and causes a compile-time warning.
C programmers will often use tagged unions, dispatching on tag values, to accomplish what ML accomplishes with datatypes and pattern matching. Nevertheless, while a C program decorated with appropriate checks will be in a sense as robust as the corresponding ML program, those checks will of necessity be dynamic; ML provides a set of static checks that give the programmer a high degree of confidence in the correctness of the program at compile time.
Note that in object-oriented programming languages, such as Java, a disjoint union can be expressed by designing class hierarchies.
Higher-order functions
Functions can consume functions as arguments:
fun applyToBoth f x y = (f x, f y)
Functions can produce functions as return values:
fun constantFn k = let
fun const anything = k
in
const
end
(alternatively)
fun constantFn k = (fn anything => k)
Functions can also both consume and produce functions:
fun compose (f, g) = let
fun h x = f (g x)
in
h
end
(alternatively)
fun compose (f, g) = (fn x => f (g x))
The function List.map from the basis library is one of the most commonly used higher-order functions in Standard ML:
fun map _ [] = [] | map f (x::xs) = f x :: map f xs
(A more efficient implementation of map would define a tail-recursive inner loop as follows:)
fun map f xs = let
fun m ([], acc) = List.rev acc
| m (x::xs, acc) = m (xs, f x :: acc)
in
m (xs, [])
end
Exceptions
Exceptions are raised with the raise keyword, and handled with pattern matching handle constructs.
exception Undefined
fun max [x] = x
| max (x::xs) = let val m = max xs in if x > m then x else m end
| max [] = raise Undefined
fun main xs = let
val msg = (Int.toString (max xs)) handle Undefined => "empty list...there is no max!"
in
print (msg ^ "\n")
end
The exception system can be exploited to implement non-local exit, an optimization technique suitable for functions like the following.
exception Zero
fun listProd ns = let
fun p [] = 1
| p (0::_) = raise Zero
| p (h::t) = h * p t
in
(p ns) handle Zero => 0
end
When the exception Zero is raised in the 0 case, control leaves the function p altogether. Consider the alternative: the value 0 would be returned to the most recent awaiting frame, it would be multiplied by the local value of h, the resulting value (inevitably 0) would be returned in turn to the next awaiting frame, and so on. The raising of the exception allows control to leapfrog directly over the entire chain of frames and avoid the associated computation.
Module system
Standard ML has an advanced module system, allowing programs to be decomposed into hierarchically organized structures of logically related type and value declarations. SML modules provide not only namespace control but also abstraction, in the sense that they allow programmers to define abstract data types.
Three main syntactic constructs comprise the SML module system: signatures, structures and functors. A structure is a module; it consists of a collection of types, exceptions, values and structures (called substructures) packaged together into a logical unit. A signature is an interface, usually thought of as a type for a structure: it specifies the names of all the entities provided by the structure as well as the arities of type components, the types of value components, and signatures for substructures. The definitions of type components may or may not be exported; type components whose definitions are hidden are abstract types. Finally, a functor is a function from structures to structures; that is, a functor accepts one or more arguments, which are usually structures of a given signature, and produces a structure as its result. Functors are used to implement generic data structures and algorithms.
For example, the signature for a queue data structure might be:
signature QUEUE = sig type 'a queue exception Queue val empty : 'a queue val isEmpty : 'a queue -> bool val singleton : 'a -> 'a queue val insert : 'a * 'a queue -> 'a queue val peek : 'a queue -> 'a val remove : 'a queue -> 'a * 'a queue end
This signature describes a module that provides a parameterized type queue of queues, an exception called Queue, and six values (five of which are functions) providing the basic operations on queues. One can now implement the queue data structure by writing a structure with this signature:
structure TwoListQueue :> QUEUE =
struct
type 'a queue = 'a list * 'a list
exception Queue
val empty = ([],[])
fun isEmpty ([],[]) = true
| isEmpty _ = false
fun singleton a = ([a], [])
fun insert (a, (ins,outs)) = (a::ins,outs)
fun peek ([],[]) = raise Queue
| peek (ins, []) = hd (rev ins)
| peek (ins, a::outs) = a
fun remove ([],[]) = raise Queue
| remove (ins, []) =
let val newouts = rev ins
in (hd newouts,([], tl newouts))
end
| remove (ins, a::outs) = (a, (ins,outs))
end
This definition declares that TwoListQueue is an implementation of the QUEUE signature. Furthermore, the opaque ascription (denoted by :>) states that any type components whose definitions are not provided in the signature (i.e., queue) should be treated as abstract, meaning that the definition of a queue as a pair of lists is not visible outside the module. The body of the structure provides bindings for all of the components listed in the signature.
To use a structure, one can access its type and value members using "dot notation". For instance, a queue of strings would have type string TwoListQueue.queue, the empty queue is TwoListQueue.empty, and to remove the first element from a queue called q one would write TwoListQueue.remove q.
One popular algorithm[2] for breadth-first traversal of trees makes uses of queues. Here we present a version of that algorithm parameterized over an abstract queue structure:
functor BFT (Q: QUEUE) = (* after Okasaki, ICFP, 2000 *)
struct
datatype 'a tree
= E
| T of 'a * 'a tree * 'a tree
fun bftQ (q : 'a tree Q.queue) : 'a list =
if Q.isEmpty q then []
else let
val (t, q') = Q.remove q
in case t
of E => bftQ q'
| T (x, l, r) => let
val q'' = Q.insert (r, Q.insert (l, q'))
in
x :: bftQ q''
end
end
fun bft t = bftQ (Q.singleton t)
end
Please note that inside the BFT structure, the program has no access to the particular queue representation in play. More concretely, there is no way for the program to, say. select the first list in the two-list queue representation, if that is indeed the representation being used. This data abstraction mechanism makes the breadth-first code truly agnostic to the queue representation choice. This is in general desirable; in the present case, the queue structure can safely maintain any of the various logical invariants on which its correctness depends behind the bulletproof wall of abstraction.
Code examples
Snippets of SML code are most easily studied by entering them into a "top-level", also known as a read-eval-print loop. This is an interactive session that prints the inferred types of resulting or defined expressions. Many SML implementations provide an interactive top-level, including SML/NJ:
$ sml Standard ML of New Jersey v110.52 [built: Fri Jan 21 16:42:10 2005] -
Code can then be entered at the "-" prompt. For example, to calculate 1+2*3:
- 1 + 2 * 3; val it = 7 : int
The top-level infers the type of the expression to be "int" and gives the result "7".
Hello world
The following program "hello.sml":
print "Hello world!\n";
can be compiled with MLton:
$ mlton hello.sml
and executed:
$ ./hello Hello world!
Insertion sort
Insertion sort for lists of integers (ascending) is expressed concisely as follows:
fun ins (n, []) = [n] | ins (n, ns as h::t) = if (n<h) then n::ns else h::(ins (n, t)) val insertionSort = List.foldr ins []
This can be made polymorphic by abstracting over the ordering operator. Here we use the symbolic name << for that operator.
fun ins' << (num, nums) = let
fun i (n, []) = [n]
| i (n, ns as h::t) = if <<(n,h) then n::ns else h::i(n,t)
in
i (num, nums)
end
fun insertionSort' << = List.foldr (ins' <<) []
The type of insertionSort' is ('a * 'a -> bool) -> ('a list) -> ('a list).
Mergesort
Here, the classic mergesort algorithm is implemented in three functions: split, merge and mergesort.
The function split is implemented with a local function named loop, which has two additional parameters. The local function loop is written in a tail-recursive style; as such it can be compiled efficiently. This function makes use of SML's pattern matching syntax to differentiate between non-empty list (x::xs) and empty list ([]) cases. For stability, the input list ns is reversed before being passed to loop.
(* Split list into two near-halves, returned as a pair.
* The “halves” will either be the same size,
* or the first will have one more element than the second.
* Runs in O(n) time, where n = |xs|. *)
local
fun loop (x::y::zs, xs, ys) = loop (zs, x::xs, y::ys)
| loop (x::[], xs, ys) = (x::xs, ys)
| loop ([], xs, ys) = (xs, ys)
in
fun split ns = loop (List.rev ns, [], [])
end
The local-in-end syntax could be replaced with a let-in-end syntax, yielding the equivalent definition:
fun split ns = let
fun loop (x::y::zs, xs, ys) = loop (zs, x::xs, y::ys)
| loop (x::[], xs, ys) = (x::xs, ys)
| loop ([], xs, ys) = (xs, ys)
in
loop (List.rev ns, [], [])
end
As with split, merge also uses a local function loop for efficiency. The inner loop is defined in terms of cases: when two non-empty lists are passed, when one non-empty list is passed, and when two empty lists are passed. Note the use of the underscore (_) as a wildcard pattern.
This function merges two "ascending" lists into one ascending list. Note how the accumulator out is built "backwards", then reversed with List.rev before being returned. This is a common technique -- build a list backwards, then reverse it before returning it. In SML, lists are represented as imbalanced binary trees, and thus it is efficient to prepend an element to a list, but inefficient to append an element to a list. The extra pass over the list is a linear time operation, so while this technique requires more wall clock time, the asymptotics are not any worse.
(* Merge two ordered lists using the order lt.
* Pre: the given lists xs and ys must already be ordered per lt.
* Runs in O(n) time, where n = |xs| + |ys|. *)
fun merge lt (xs, ys) = let
fun loop (out, left as x::xs, right as y::ys) =
if lt (x, y) then loop (x::out, xs, right)
else loop (y::out, left, ys)
| loop (out, x::xs, []) = loop (x::out, xs, [])
| loop (out, [], y::ys) = loop (y::out, [], ys)
| loop (out, [], []) = List.rev out
in
loop ([], xs, ys)
end
The main function.
(* Sort a list in according to the given ordering operation lt.
* Runs in O(n log n) time, where n = |xs|.
*)
fun mergesort lt xs = let
val merge' = merge lt
fun ms [] = []
| ms [x] = [x]
| ms xs = let
val (left, right) = split xs
in
merge' (ms left, ms right)
end
in
ms xs
end
Also note that the code makes no mention of variable types, with the exception of the :: and [] syntax which signify lists. This code will sort lists of any type, so long as a consistent ordering function lt can be defined. Using Hindley–Milner type inference, the compiler is capable of inferring the types of all variables, even complicated types such as that of the lt function.
Quicksort
Quicksort can be expressed as follows. This generic quicksort consumes an order operator <<.
val filt = List.filter
fun quicksort << xs = let
fun qs [] = []
| qs [x] = [x]
| qs (p::xs) = let
val lessThanP = (fn x => << (x, p))
in
qs (filt lessThanP xs) @ p :: (qs (filt (not o lessThanP) xs))
end
in
qs xs
end
Expression language
Note the relative ease with which a small expression language is defined and processed.
exception Err
datatype ty
= IntTy
| BoolTy
datatype exp
= True
| False
| Int of int
| Not of exp
| Add of exp * exp
| If of exp * exp * exp
fun typeOf (True) = BoolTy
| typeOf (False) = BoolTy
| typeOf (Int _) = IntTy
| typeOf (Not e) = if typeOf e = BoolTy then BoolTy else raise Err
| typeOf (Add (e1, e2)) =
if (typeOf e1 = IntTy) andalso (typeOf e2 = IntTy) then IntTy else raise Err
| typeOf (If (e1, e2, e3)) =
if typeOf e1 <> BoolTy then raise Err
else if typeOf e2 <> typeOf e3 then raise Err
else typeOf e2
fun eval (True) = True
| eval (False) = False
| eval (Int n) = Int n
| eval (Not e) =
(case eval e
of True => False
| False => True
| _ => raise Fail "type-checking is broken")
| eval (Add (e1, e2)) = let
val (Int n1) = eval e1
val (Int n2) = eval e2
in
Int (n1 + n2)
end
| eval (If (e1, e2, e3)) =
if eval e1 = True then eval e2 else eval e3
fun chkEval e = (ignore (typeOf e); eval e) (* will raise Err on type error *)
Arbitrary-precision factorial function (libraries)
In SML, the IntInf module provides arbitrary-precision integer arithmetic. Moreover, integer literals may be used as arbitrary-precision integers without the programmer having to do anything.
The following program "fact.sml" implements an arbitrary-precision factorial function and prints the factorial of 120:
fun fact n : IntInf.int =
if n=0 then 1 else n * fact(n - 1)
val () =
print (IntInf.toString (fact 120) ^ "\n")
and can be compiled and run with:
$ mlton fact.sml $ ./fact 66895029134491270575881180540903725867527463331380298102956713523016335 57244962989366874165271984981308157637893214090552534408589408121859898 481114389650005964960521256960000000000000000000000000000
Numerical derivative (higher-order functions)
Since SML is a functional programming language, it is easy to create and pass around functions in SML programs. This capability has an enormous number of applications. Calculating the numerical derivative of a function is one such application. The following SML function "d" computes the numerical derivative of a given function "f" at a given point "x":
- fun d delta f x =
(f (x + delta) - f (x - delta)) / (2.0 * delta);
val d = fn : real -> (real -> real) -> real -> real
This function requires a small value "delta". A good choice for delta when using this algorithm is the cube root of the machine epsilon.
The type of the function "d" indicates that it maps a "float" onto another function with the type "(real -> real) -> real -> real". This allows us to partially apply arguments. This functional style is known as currying. In this case, it is useful to partially apply the first argument "delta" to "d", to obtain a more specialised function:
- val d = d 1E~8; val d = fn : (real -> real) -> real -> real
Note that the inferred type indicates that the replacement "d" is expecting a function with the type "real -> real" as its first argument. We can compute a numerical approximation to the derivative of 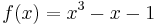 at
at 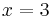 with:
with:
- d (fn x => x * x * x - x - 1.0) 3.0; val it = 25.9999996644 : real
The correct answer is 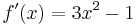 =>
=>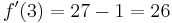 .
.
The function "d" is called a "higher-order function" because it accepts another function ("f") as an argument.
Curried and higher-order functions can be used to eliminate redundant code. For example, a library may require functions of type a -> b, but it is more convenient to write functions of type a * c -> b where there is a fixed relationship between the objects of type a and c. A higher order function of type (a * c -> b) -> (a -> b) can factor out this commonality. This is an example of the adapter pattern.
Discrete wavelet transform (pattern matching)
The 1D Haar wavelet transform of an integer-power-of-two-length list of numbers can be implemented very succinctly in SML and is an excellent example of the use of pattern matching over lists, taking pairs of elements ("h1" and "h2") off the front and storing their sums and differences on the lists "s" and "d", respectively:
- fun haar l = let
fun aux [s] [] d = s :: d
| aux [] s d = aux s [] d
| aux (h1::h2::t) s d = aux t (h1+h2 :: s) (h1-h2 :: d)
| aux _ _ _ = raise Empty
in
aux l [] []
end;
val haar = fn : int list -> int list
For example:
- haar [1, 2, 3, 4, ~4, ~3, ~2, ~1]; val it = [0,20,4,4,~1,~1,~1,~1] : int list
Pattern matching is a useful construct that allows complicated transformations to be represented clearly and succinctly. Moreover, SML compilers turn pattern matches into efficient code, resulting in programs that are not only shorter but also faster.
Implementations
Many SML implementations exist, including:
- MLton is a whole-program optimizing compiler that produces very fast code compared to other ML implementations. [1]
- Poly/ML is a full implementation of Standard ML that produces fast code and supports multicore hardware (via Posix threads).
- Standard ML of New Jersey (abbreviated SML/NJ) is a full compiler, with associated libraries, tools, an interactive shell, and documentation. [2]
- Moscow ML is a light-weight implementation, based on the CAML Light runtime engine. It implements the full SML language, including SML Modules, and much of the SML Basis Library. [3]
- TILT is a full certifying compiler for SML. It uses typed intermediate languages to optimize code and ensure correctness, and can compile to typed Assembly language.
- HaMLet is an SML interpreter that aims to be an accurate and accessible reference implementation of the standard.
- The ML Kit integrates a garbage collector (which can be disabled) and region-based memory management with automatic inference of regions, aiming realtime applications. Its implementation is based very closely on the Definition.
- SML.NET allows compiling to the Microsoft CLR and has extensions for linking with other .NET code.
- SML2c is a batch compiler and compiles only module-level declarations (i.e. signatures, structures, functors) into C. It is based on SML/NJ version 0.67 and shares the front end, and most of its run-time system, but does not support SML/NJ style debugging and profiling. Module-level programs that run on SML/NJ can be compiled by sml2c with no changes.
- The Poplog system implements a version of SML, with POP-11, and optionally Common Lisp, and Prolog, allowing mixed language programming. For all, the implementation language is POP-11, which is compiled incrementally. It also has an integrated Emacs-like editor that communicates with the compiler.
- SML# is a conservative extension of SML providing record polymorphism and C# interoperability.
- Alice: an interpreter for Standard ML by Saarland University adding features for lazy evaluation, concurrency (multithreading and distributed computing via remote procedure calls) and constraint programming.
All of these implementations are open-source and freely available. Most are implemented themselves in SML. There are no longer any commercial SML implementations. Harlequin once produced a commercial IDE and compiler for SML called MLWorks. The company is now defunct. MLWorks is believed to have been passed on to Xanalys.
See also
References
External links
- What is SML?
- What is SML '97?
- successor ML (sML) is intended to provide a vehicle for the continued evolution of ML, using Standard ML as a starting point.
- Standard ML language at Scholarpedia, curated by Mads Tofte.